Editor’s Note: The paper on which this article is based was originally presented at the 2020 IEEE International Symposium on Electromagnetic Compatibility & Signal/Power Integrity (EMC, SI & PI), where it received recognition as the Best Symposium Paper. It is reprinted here with the gracious permission of the IEEE. Copyright 2021 IEEE.
Introduction
Contents
CISPR Publication 24 [1] allows the use of 1% or 4% frequency steps when testing a product for immunity to both radiated RF disturbances and conducted RF disturbances in the frequency range from 150 kHz to 1 GHz. When testing using 4% steps, the disturbance voltage level is doubled. This is a 6 dB increase. CISPR Publication 35 [2] has carried forward the same testing option. CISPR 35 currently includes spot frequency tests above 1 GHz rather than swept frequency tests. However, other standards such as the ETSI EN 301 489‑1 [3] implement swept frequency testing above 1 GHz. A swept frequency test from 1 GHz to 6 GHz is under consideration for inclusion in a future edition of CISPR 35.
During a February 2018 meeting of CISPR/I Maintenance Team 8 (MT8), a discussion about the necessity of 4% steps for certain products led to the question of whether it is valid to allow 4% testing at twice the disturbance level. Some of the experts expressed concern that this is a relaxation in the standard since susceptibilities could be missed using the wider step size.
The work described in this paper was carried forward in response to that good question. Much of the material from the section of this paper on “Observed Contours Below 1 GHz” was presented during the October 2018 MT8 meeting. The MT8 experts asked for the data to be made more visible to peers, both as a formal CISPR/I working document and for broad review in a technical forum like an IEEE EMC Society conference or publication. They also asked for further work looking to see whether the patterns observed below 1 GHz also applied above 1 GHz should swept testing be implemented in a future edition of CISPR 35 or other CISPR standards.
This paper presents a portion of what was presented to MT8 on the contours or shapes of radiated susceptibilities between 80 MHz and 1 GHz. This paper also presents new data on the shape of susceptibilities above 1 GHz. While the 4% frequency step option is allowed for both radiated and conducted immunity testing, this paper looks only at radiated immunity using data taken at the HP Vancouver EMC Engineering Lab, where both authors worked at the time.
Susceptibility Contours
In many EMC test labs, a radiated immunity test is performed at the regulatory limit, and it either passes or fails. In the HP Vancouver lab, testing is typically performed at twice the required field strength using 1% frequency steps to demonstrate design margin. The lab’s common process when a susceptibility is found is to characterize the range and depth of the weakness.
The regular 1% step process tells us the lower end of the failure range. The operator will select a frequency many steps higher in frequency until he or she finds a frequency where the EUT again would pass at the doubled field strength. Then the disturbance frequency is lowered in 1% steps until the highest susceptible frequency is identified. To gain more data about the susceptibility contour, the same process might be run with the disturbance level lowered to the required field strength. For further insight, at several frequencies within the susceptible range a step attenuator in the RF signal path would be used to significantly lower the disturbance field strength. Then the field is raised in 1 dB steps to find the susceptible field strength at that frequency. This kind of investigation is repeated at several frequencies within the susceptible range.
The result is a susceptibility contour: a set of data showing the shape of the field strengths at which a product will pass or fail at multiple frequencies. Figure 1 is an example of such a contour. The horizontal axis counts 1% frequency steps making it a logarithmic axis for frequency, while the vertical axis is field strength in linear units. The blue dots represent the field strength data at each frequency step tested within the susceptible range. It is plotted at the highest level where the EUT ‘passed’ by showing Criterion A performance. The superimposed brown curve and the number 4598 will be explained later in this paper.
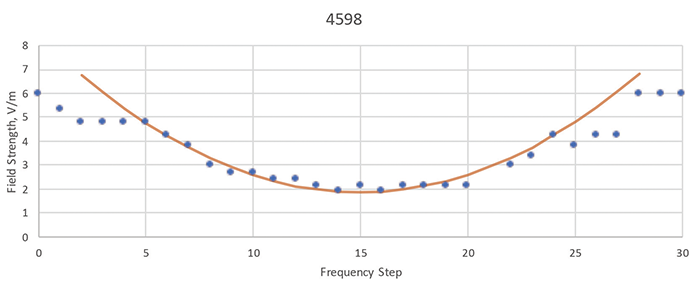
Figure 1: Sample susceptibility contour
Since these anomalies can occur anywhere in the tested frequency range, the left-most data point is not the 80 MHz frequency where the test starts. Rather, it is a frequency step just below the lower edge of the susceptible range. This makes the contour easier to see. Outside the susceptible range, the blue dots will be at 6 V/m, since that is the highest field strength tested. The actual susceptible level may be higher.
This measurement process takes effort. It is a useful way to compare the susceptibilities across multiple test samples to understand manufacturing variability. This data also allows designers to understand more clearly how a proposed remedy is affecting the underlying issue in frequency and depth. It provides a richer view of what is happening in the EUT than merely a binary pass or fail result.
Characterizing the Contours
When the question was asked at that MT8 meeting in early 2018, we realized we had a unique library of information on our data drives that could add to the shared understanding of the way real electronic devices are susceptible to RF disturbances. Our answer could have been simple: in all the historic test data we reviewed, every test sample that failed the 3 V/m test also failed the 6 V/m test on at least four consecutive 1% steps. Thus, any EUT that passed the 4% test would also have passed the 1% test. Furthermore, in our data sets are many test samples that would have failed the 4% test but passed the 1% test. This data says the 4% test is not a relaxation. It is a more stringent test.
That would have been the simple conclusion. But we wanted to probe deeper.
The better question is about the shape of these susceptibility contours. Do they tend to be narrowband or broadband? That’s the key physics question for whether 4% steps are valid. If we think about this in RF Engineering terms, we consider the underlying resonance of an unintended bandpass filter and ask: Is the susceptibility coupled through structures and circuits with high-Q or low-Q resonances?
Our simple model for that question is to apply a 3-point parabolic fit to the data. We start with the equation
v = af2 + bf + c (1)
where v is the highest disturbance level for a passing result at frequency step f, with a, b, and c being constants derived from the test data. Note that f is treated as a unitless step number, not a direct frequency in Hz units, because we are interested in the shape of a susceptibility with reference to ratio step spacing.
If we pick a set of three radiated immunity data points {(F1 V1), (F2 V2), (F3 V3)} we can compute the parameters a, b, and c as follows. It is helpful to first calculate an intermediate constant k.
k = (F1 – F3)/(F2 – F3) (2)
a = [V1 – kV2 + (k-1)V3]/[F12 + (k-1)F32] (3)
b = [V2 – V3 – a(F22 – F32)]/(F2 – F3) (4)
c = V1 – aF12 – bF1 (5)
The brown parabola shown in Figure 1 was calculated by selecting three data points, applying (2) through (5) to calculate the critical parameters of a parabola passing through those points and then plotting the resulting parabola using (1). The same process was applied to each data set reported in this paper.
The shape of any parabola is determined by the parameters a, b, and c for that parabola. Parameter a sets the width of the parabola, while b and c together shift the parabola up, down, left, and right. It is the parameter a that will help us understand how narrow or broad is the susceptibility response of an EUT. If a is large, then the parabola is narrow. This means that the EUT circuits or structures that participate in the susceptibility are highly resonant, and the 4% step size may miss some susceptibility that the 1% step size would find. If a is small, the parabola is wide. This tells us that the EUT is not strongly resonant and the 4% method will work just fine.
Figure 2 shows the theoretical limiting case. In this situation, the susceptibility is just wide enough to touch two adjacent 4% steps at the 6 V/m level, and deep enough to touch the 3 V/m level. Make the parabola any wider, and the 4% case would always catch the susceptibility even when the 3 V/m test does not. Make it any narrower, and the EUT might fail at 3 V/m but pass at 6 V/m. In this Figure, a has the value 0.75.

Figure 2: Theoretical limit case for 4% step size validity
If a class of products consistently shows values of a smaller than 0.75, then the 4% step option is valid for those products and is at least as rigorous as the 1% step option.
Observed Contours Below 1 GHz
The data in Table 1 are from a variety of products tested in two randomly selected date ranges: November 2001 to June 2002, and June 2009 through August 2010. We will not indicate whether the samples were early prototypes or near-production units, nor will we identify the EUT other than by the internal project number. The table also indicates the number of frequency steps where anomalies were observed, the approximate center frequency of the susceptible range, and the depth of the susceptibility below the 6 V/m target level.
| Project | a value | Center Freq. | Width | Depth |
| 4598 | 0.029 | 152.7 MHz | 27 steps | 10 dB |
| 5432 | 0.075 | 193.4 MHz | 23 steps | 9 dB |
| 5381 | 0.040 | 139.3 MHz | 23 steps | 12 dB |
| 5498 | 0.169 | 82.9 MHz | 8 steps | 8 dB |
| 5811 | 0.195 | 179.2 MHz | 5 steps | 3 dB |
| 5825 | 0.033 | 187.3 MHz | 19 steps | 8 dB |
| 30004 | 0.040 | 271.8 MHz | 18 steps | 10 dB |
| 30100 | 0.677 | 390.3 MHz | 17 steps | 4 dB |
| 30204 | 0.060 | 94.8 MHz | 9 steps | 2 dB |
Table 1: Summary of results below 1 GHz
These EUTs are from a variety of office products including printers and scanners for home and small office use or for commercial use. No product was tested within the receive band of an intentional radio receiver, since radio receivers are designed to respond to RF signals within their tuned frequency bands. No product model is presented twice, but the most complete contour is shown for each product model tested within those date ranges where a radiated susceptibility was observed. A few susceptibility contours are included as Figures 3 through 5. The internal project number is indicated at the top of each graph and in the caption, for correlation with the Table 1 entries. The brown curve in each Figure is the parabola passing through three data points and its width corresponds to the a value shown in Table 1.
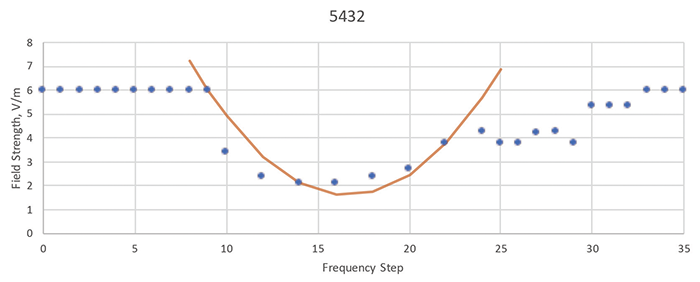
Figure 3: Susceptibility contour and parabolic curve fit from project 5432
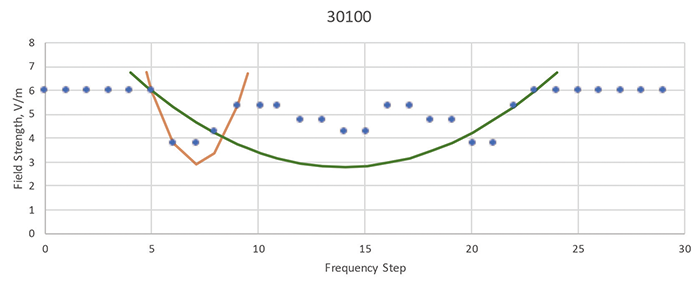
Figure 4: Susceptibility contour and parabolic curve fit from project 30100
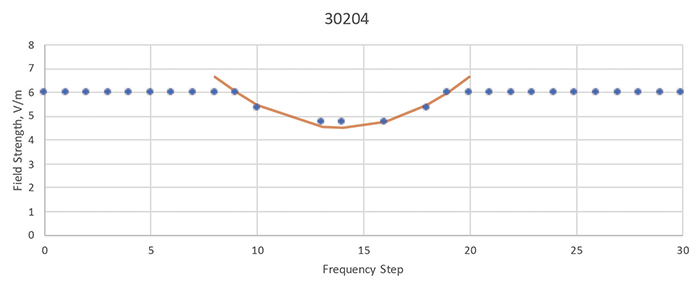
Figure 5: Susceptibility contour and parabolic curve fit from project 30204
In all but one of these cases, the a value is much lower than 0.75. The one outlier is project 30100 where the a value listed in Table 1 is 0.677, just below 0.75. That test showed a rippling susceptibility curve that doesn’t match a parabola well. This a value is based on the brown curve in Figure 4 which traces just one of the ripples. An equally valid interpretation of that susceptibility contour is the green parabola in Figure 4, which leads to an a value of 0.040. Parabolic curve matching is useful, even if it is not perfect.
Assembling a Benchtop Setup for Experimenting Above 1 GHz
The data in Table 1 are from regular product testing. This lab has no history of test projects that failed radiated immunity testing above 1 GHz. To investigate this part of the spectrum, we set up a special test environment to explore the frequency range 1 GHz to 2 GHz at much higher field levels.
We assembled a benchtop system that could be used in place of the full chamber configuration. This was done so that we could experiment in a way that would not tie up the main test facility. Between experiment sessions, the benchtop assembly could be rolled into storage in under 5 minutes. We were aiming our experiments toward small, inexpensive EUTs since products might be damaged or destroyed by disturbances at approximately 20 times the usual field levels. We were hopeful that we could quickly and inexpensively identify samples that had anomalies we could study. Our benchtop system includes an HP83623B Swept Signal Generator that allowed precise control of frequency, amplitude, sweep time, and modulation. This allowed us to explore devices quickly and then further investigate using precise, small steps to develop susceptibility contours for the ones that showed non-destructive anomalies. These small steps are much smaller than the 1% or 4% steps discussed so far. The steps used are over-sampling compared to a test performed according to the test standards already mentioned.
Our intent was to find interesting cases, hoping that we could understand the width of the susceptibilities and project or scale our results to the 3 V/m and 6 V/m test modes. This seems easier than having to find real products that are sensitive to fields below 6 V/m. As the data in section VI will show, we saw anomalous details that would have been missed, hidden, or otherwise obscured in standard testing.
Figure 6 shows some of the test hardware used to explore the susceptibility contours of two samples at these higher frequencies. A carrier at a maximum level of ‑25 dBm was 80% AM-modulated and fed into the amplifier. The amplifier output was sent into a small TEM cell, an FCC-TEM-JM2. The second coaxial port on the cell was loaded with an RF attenuator, and the attenuated signal was sent to a spectrum analyzer for additional monitoring. This allowed us to drive the test fields well above the CISPR 24 or CISR 35 disturbance levels and find some anomalous behaviors. The testing was performed manually, with the frequency stepped in 1 MHz increments, not 1% increments. However, analysis to find a was done based on the fractional 1%‑step value calculated for each test frequency.

Figure 6: Test equipment used for evaluations above 1 GHz
The IEC 61000-4-3 [4] test method describes the field strength based on the carrier level before modulation is added. Our estimate was that a -25 dBm unmodulated carrier from the signal generator produced an unmodulated field within the TEM around 117 V/m. With the effect of modulation added, we estimate that the same drive strength yields a peak field strength above 200 V/m. Those are the levels of disturbance field we used in hopes of finding susceptibilities to study in this frequency range.
The TEM we have is designed for testing integrated circuits. The top surface is a square metal plate that can be removed to place a sample inside. The plate can also be replaced with a custom fixture that accommodates the test sample. The device is 34 cm long, and its manufacturer states it can accept an EUT up to 6 cm x 6 cm x 1 cm.
We used two samples in this study. The first was a 16 GByte USB memory drive shown in Figure 7. Part of the plastic housing was removed. In this case, we used a top plate with a hole through which we ran the USB cable. The cable shield was bonded to the metal plate with foil tape which also sealed the TEM. The plate was then inverted as shown in Figure 8, so that the drive was inside the sealed TEM and only the USB cable emerged. The cable was connected to a computer. The drive was exercised with repeated read-write-verify cycles.

Figure 7: USB memory drive inserted through the metal plate

Figure 8: TEM cell closed with the USB cable merging
The second sample was a small mobile flip phone as pictured in Figure 9. It was small enough to fit entirely within the TEM with no attached cables. It was exercised by repeatedly playing music files stored in internal memory. We listened for the music to stop playing in response to the disturbance field.

Figure 9: Flip phone placed in the TEM cell
This test method does not give us calibrated field values, and it isn’t a standard test environment. These test samples may be large enough to distort the fields in this small TEM. Our goal was to excite a susceptibility then to measure the shape of the contour across a range of frequencies to see the degree of resonance involved. That only required relative measurements, which are still feasible in a nonstandard uncalibrated overloaded fixture. Relative measurements only require that the test system be linear with applied power and across a narrow range of frequencies. We believe this benchtop system remained linear over the frequency and amplitude ranges used.
Observed Contours Above 1 GHz
This experiment found one set of anomalies for each test sample. The susceptibility contours are shown in Figures 10 and 11. The data is characterized in Table 2. No test samples were damaged by the strong field levels used in these experiments.
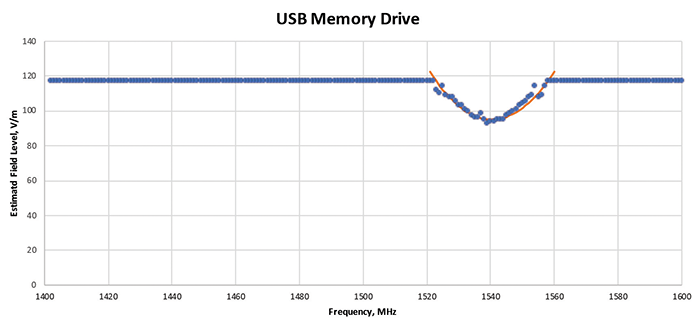
Figure 10: USB drive susceptibility contour and parabolic curve fit

Figure 11: Mobile phone susceptibility contour and parabolic curve fit
| Sample | a value | Center Freq. | Width | Depth |
| USB drive | 0.87 | 1541 MHz | 2.22 steps | 2 dB |
| Phone | 2.57 | 1958 MHz | 3.03 steps | 18 dB |
Table 2: Summary of results above 1 GHz
In Figures 10 and 11, the frequency axis is a linear axis with data points separated by 1 MHz. The USB memory drive had a contour that is reasonably modeled with a parabola. The mobile phone demonstrated a very erratic contour that does not seem to match any simple function. It showed anomalies with applied fields in the vicinity of 20 to 60 V/m. Both of the a values observed are well above the reference of 0.75, indicating that a 4% step size for these test items in this frequency range could miss an anomaly.
To calculate the parabolas in Figures 10 and 11 and the data in Table 2 consistent with the earlier sections, the amplitude data had to be translated to a 6-unit linear scale, and the frequency data converted to 1% step values.
The frequency was converted to step values assuming the starting test frequency is 1000 MHz. During 1% steps the frequency increases by repeated factors of 1.01. A linear frequency G, in MHz, is converted to a numeric step value, F, using (6).
F = (log10G – log101000)/log101.01 (6)
The signal amplitudes H, originally in dBm, were converted to linear voltage values, V, using (7).
V = 10(H + 40.56)/20 (7)
A factor of 40.56 dB in (7) controls the scaling. With this conversion factor, ‑25 dBm maps to 6 linear voltage units and ‑31 dBm maps to 3 linear voltage units. A similar equation with a different scaling factor leads to the estimated actual field strength of 117 V/m.
Discussion of Results
The data in the lower frequency range supports the full validity of 4% step testing at twice the disturbance level. The second data set in the higher frequency range does not.
We should acknowledge some of the weaknesses of our data. This data set is somewhat limited by the kinds of anomalies that have been observed in our lab. We have not seen radiated immunity failures centered at frequencies above 400 MHz. We have simulated some anomalies above 1 GHz, but these are at field levels well above the standard test levels for these multimedia devices. At these disturbance levels, different effects could be at play from what is excited by fields at the typical CISPR 35 test level of 3 V/m.
This data leaves us unable to state anything reliable about what a typical susceptibility contour would look like in the range from 400 MHz to 1 GHz.
We add, for discussion, Figures 12 and 13 to simulate 1% step test results. These two plots are drawn from the same basic data shown in Figures 10 and 11 with the following modifications. First, the vertical axis data is scaled for presentation against a 6-voltage-unit maximum test level implying a ‘limit’ of 3 voltage units. Second, the horizontal scale is now step numbers. This axis counts 1% steps starting at 1 GHz, which is numbered step zero when using (6). Finally, all the data points that lie between the 1% step frequencies were omitted. Since each parabola was calculated based on the full data set, it may no longer pass through three visible data points.
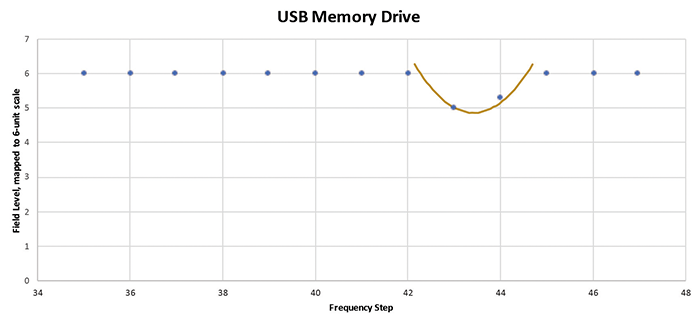
Figure 12: USB drive susceptibility data scaled and reduced to 1% steps
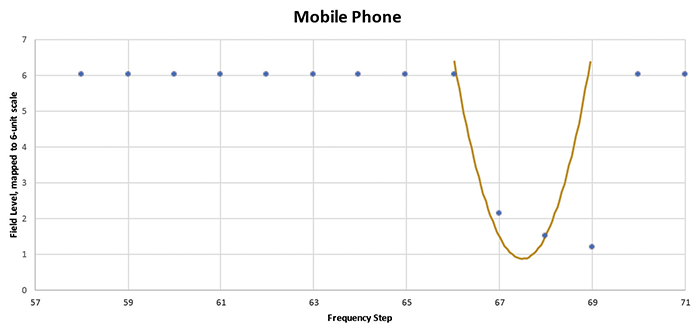
Figure 13: Mobile phone susceptibility data scales and reduced to 1% steps
A few observations come from this revised analysis of the data. The first is that the mobile phone has a lot of fine detail in its susceptibility curve that is lost in even a 1% step test. Compare Figure 11 to Figure 13. Selecting only the 1% step data, we see some odd and erratic steps, very much like we saw in some of the data below 1 GHz reported in section IV. This causes us to wonder what fine detail might have been available from the test samples shown in Figures 3 and 4 had those tests used a smaller step size.
Second, we realize that statistics are fickle on small sample sizes. Most radiated immunity tests are done with a sample size of one. The memory drive and mobile phone had narrow susceptibilities, with a values greater than 0.75. We have shown that a 4% step test might have missed a susceptibility that appears over such a narrow frequency range. That does not necessarily mean the 4% step test is a relaxed standard or that a narrowband weakness will be missed. The memory drive would have failed the 6-unit 4% test at the twelfth frequency (step 44) but passed the 3-unit 1% test with no anomalies. The phone would have failed the 3-unit 1% test at three frequencies, steps 67, 68, and 69. As luck would have it, the 4% test would have found the susceptibility at step 68. For these two samples, the 4% frequency step test at twice the test level would have detected more EUT weaknesses than the 1% step test. Yet with a slight frequency shift, there is a fair chance that the deep mobile phone weakness could have been entirely missed using the 4% step method.
Finally, we will note that the parabolic fit was not selected due to any specific analysis of why radiofrequency immunity failures occur. It would be rash to suppose that all susceptibilities have the same kinds of underlying failure mechanisms, so we do not suggest that the parabola comes from a physics-based model. The parabola is simply a gauge we selected because it is based on easily solvable math, and it seems to match some of the data well enough to provide a useful way to think about these disparate data sets. We shouldn’t assume that the selection of 1% frequency steps was based on some prior rigorous analysis of RF test failure mechanisms, either. Engineering is often an intersection of math, physics, and practicality.
Areas for Further Study
There seems to be little public information about the typical susceptibility profiles for electronic equipment. This kind of data may be held privately and kept confidential for fear that it might be misunderstood as a product or brand weakness. If others have examined the width and depth of product susceptibilities, we encourage publication of those data so that the standards development organizations can optimize the test processes to match actual types of issues and threats faced by electronic products.
The authors of this paper particularly welcome further data covering additional product families and additional frequency bands. We hope that colleagues who see immunity issues at these higher frequencies and at standard test levels will spend the additional few hours required to measure the breadth and depth of the issues. While one sample might not make a good conference paper, we would be happy to help several individuals with one sample each combine their efforts into a joint paper.
This paper has focused on radiated immunity testing, and the same questions exist regarding conducted susceptibility from 150 kHz to 80 MHz. We are unable to report on the shape of conducted immunity profiles because we have rarely seen issues in that test. We simply do not have contour data sets from that frequency range. If other labs see conducted susceptibilities, we hope they will explore and report on the contours of those susceptibilities using methods like those we have described.
Absent data that characterizes swept immunity issues, we are all left to theorize about how well the 4% step processes – or even a 1% step process – will find typical product weaknesses.
If the absence of good data at higher frequencies is because products rarely have susceptibilities at higher frequencies, that would also be important to know. A lot of time and money is spent each year doing radiated immunity testing from 1 to 6 GHz. If there are no anomalies being found, then our profession may wish to reconsider the practical value of that testing on products that are not safety-critical or mission-critical.
This data suggests a general pattern that 4% steps are fine below 400 MHz but perhaps not above 1 GHz. We welcome researchers to share data on anomalies in the intervening range to help our profession understand where between 400 MHz and 1 GHz that changes, and perhaps help explain why.
Conclusion
CISPR 24 and CISPR 35 allow two methods of swept frequency immunity testing: 1% frequency steps at the specified disturbance level, and 4% steps at twice that disturbance level. The data presented here suggests that testing with the 4% step method will reliably find radiated susceptibilities in multimedia equipment at frequencies below 400 MHz but may not always find those that exist above 1 GHz. The authors can draw no conclusions regarding the effectiveness of the 4% step method in the frequency range from 400 MHz to 1 GHz due to a lack of product issues observed in this frequency range.
References
- CISPR Publication 24: Information technology equipment – Immunity characteristics – Limits and methods of measurement, Ed. 2.1. Geneva: IEC, 2015.
- CISPR Publication 35: Electromagnetic compatibility of multimedia equipment – Immunity requirements, Ed. 1. Geneva: IEC, 2016.
- ETSI/EN 301 489-1: ElectroMagnetic Compatibility (EMC) standard for radio equipment and services; Part 1: Common technical requirements; Harmonised Standard for ElectroMagnetic Compatibility, V2.2.1 (draft). Sophia Antipolis, France: ETSI, 2019.
- IEC 61000-4-3: Electromagnetic compatibility (EMC) – Part 4-3: Testing and measurement techniques – Radiated, radio-frequency, electromagnetic field immunity test, Ed. 3.2. Geneva: IEC, 2010.


