Analog IQ Modulators (for transmitters) and IQ Demodulators (for receivers) have been used for decades ([1] to [3]).
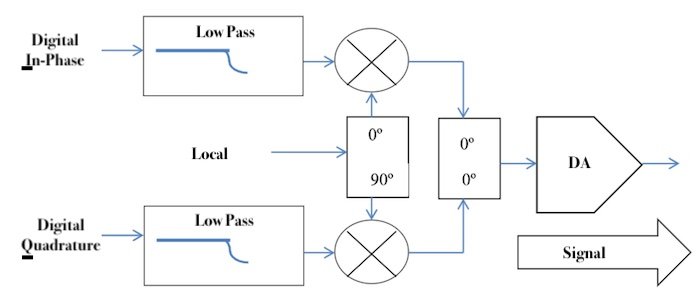
the Recently, new A/D and D/A Converters have been introduced, which can directly sample an IF at from 1 to 4 GHz; sampling in the 2nd, 3rd, and 4th Nyquist zones ([4] to [7]). These, combined with higher speed digital logic, allow the combining (for A/D) and separation (for D/A) do be done digitally ([8] to [21]). This is illustrated in Figure 1(a) (for a modulator) and Figure 1(b) (for a demodulator) with the Data Converter (DAC or ADC) in position “D”.
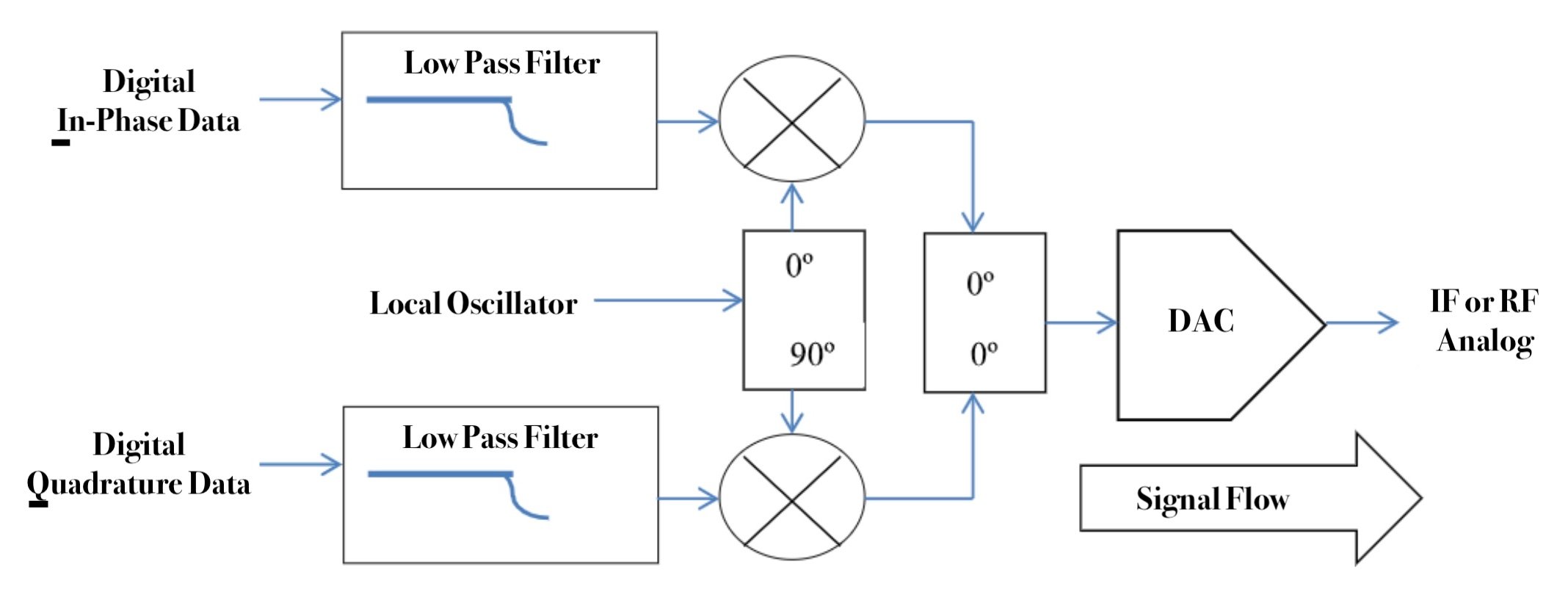
Figure 1(a). Modulator
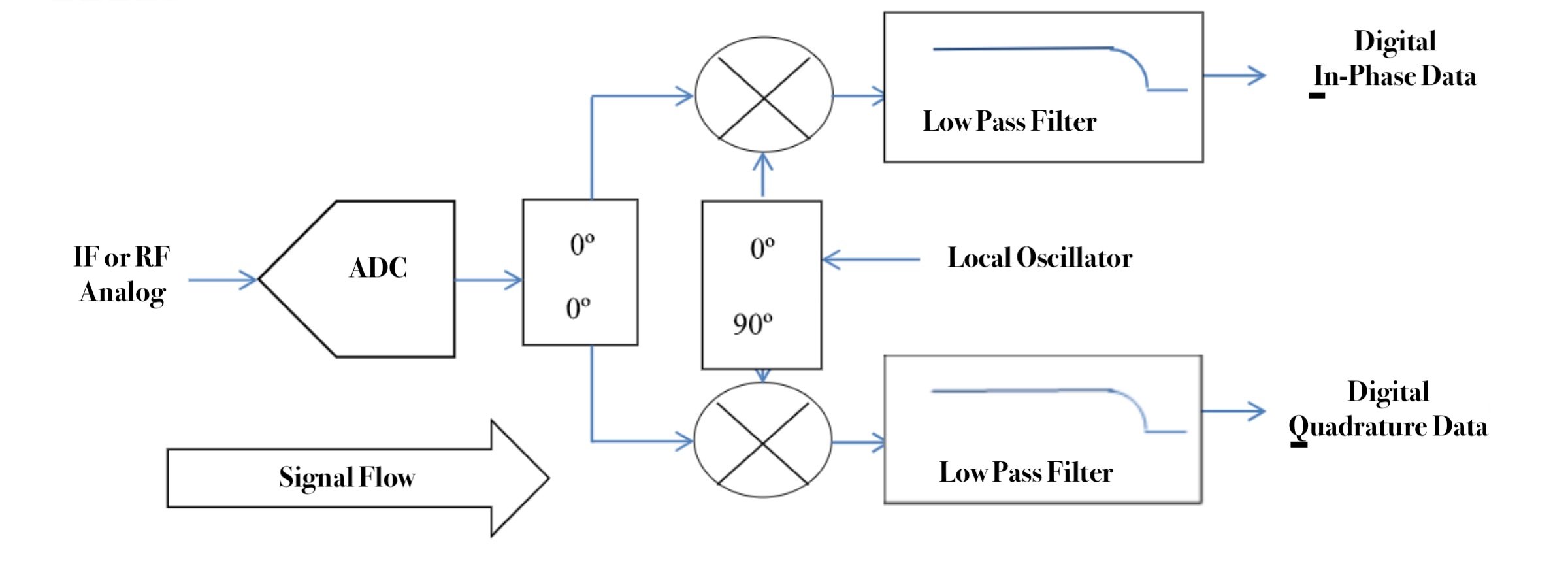
Figure 1(b). Demodulator
On the other hand, integrated analog I, Q combiners and separators have very good matching between the I and Q paths, solving some of the objections to doing these processes analogly. The analog technique also requires twice the data converters (A/Ds or D/As) than direct sampling at IF, but they run at lower sampling rates; so they are cheaper and require less power. This is illustrated in Figure 1(a) (for a modulator) and Figure 1(b) (for a demodulator) with the Data Converter (DAC or ADC) in position “A”.
The author starting thinking about this question. He asked for opinions on several LinkedIn groups, and received valuable answers. With the approval of the acknowledgees, they are acknowledged below. He also found out whatever information he could on the properties of contemporary Integrated Circuits (ICs) for these functions, and the results of whatever performance requirements had been determined for these ICs. From this, he tried to generate whatever general conclusions could be drawn to answer the question; “Should IQ Modulation and Demodulation be done Analogly or Digitally?”
Analog IQ Approach
The analog IQ approach has been around for decades ([1] to [3]). Any IF or RF signal can be represented by
R(t) = I(t)cos(2πft) +Q(t)sin(2πft)
where f is the carrier frequency, I(t) is called the In-Phase component, and Q(t) is called the Quadrature component. An analog IQ modulator takes the baseband signals I(t) and Q(t) and forms R(t). This is shown in Figure 1(a) with the DACs in position A. An analog IQ demodulator takes as input R(t), and forms I(t) and Q(t). This is shown in Figure 1(b) with the DACs in position A.
A critical problem with the analog approach is maintaining the gains through the two paths to be identical, and the phase difference to be exactly 90º. Sometimes neglected for these requirements are the two Low Pass Filters. They should be exactly gain and phase-matched for all frequencies where there is significant signal energy. More exact quantification of these requirements, and the impairments caused by deviations from them, are shown in a later article.
Digital IQ Approach
Recent developments in high-speed data converters (DACs and ADCs), have lead people to avoid the IQ imbalance problem discussed in the Analog IQ Approach section by implementing the IQ Modulator and Demodulator functions digitally, where the gain and phase can be produced with no error ([5], [8] to [21]). For the modulator case, there is a high-speed DAC at the output, as shown in Figure 1(a) with the DAC in position D. For the demodulator case, there is a high-speed ADC at the input, as shown in Figure 1(b) with the ADC in position B.
Often these digital approaches take advantage of the aliasing effect, using what is called bandpass sampling ([22] to [24]. [24A], [24B]). Figure 2(a) shows a waveform sampled in time. Figure 2(b) shows the spectra of the unsampled and sampled signal. The sample clock of the ADC is performing the same function as the Local Oscillator in an RF mixer. For an ADC, an analog filter can allow only a signal in one Nyquist zone to pass, and this mixing action can be used to downconvert a signal in that Nyquist zone to baseband.
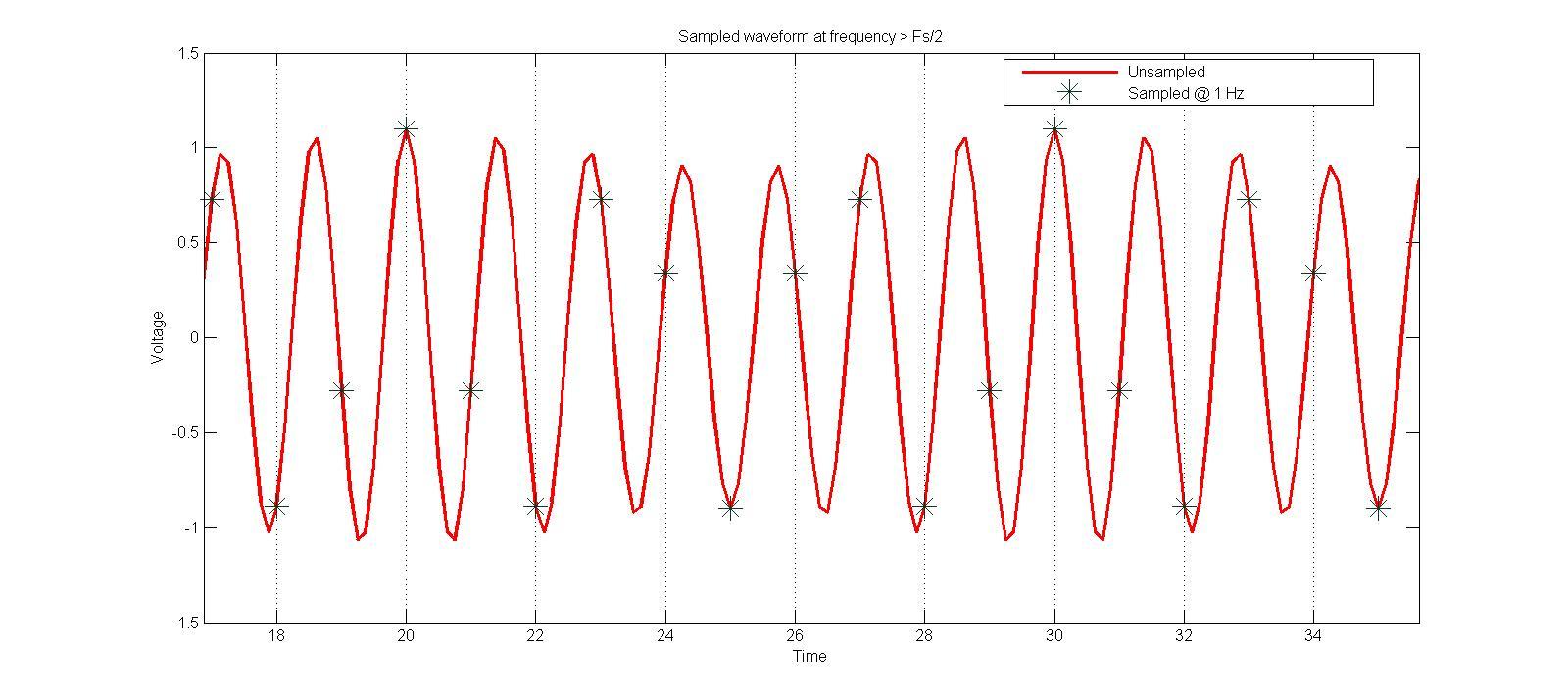
Figure 2(a). Sampling in Time Domain
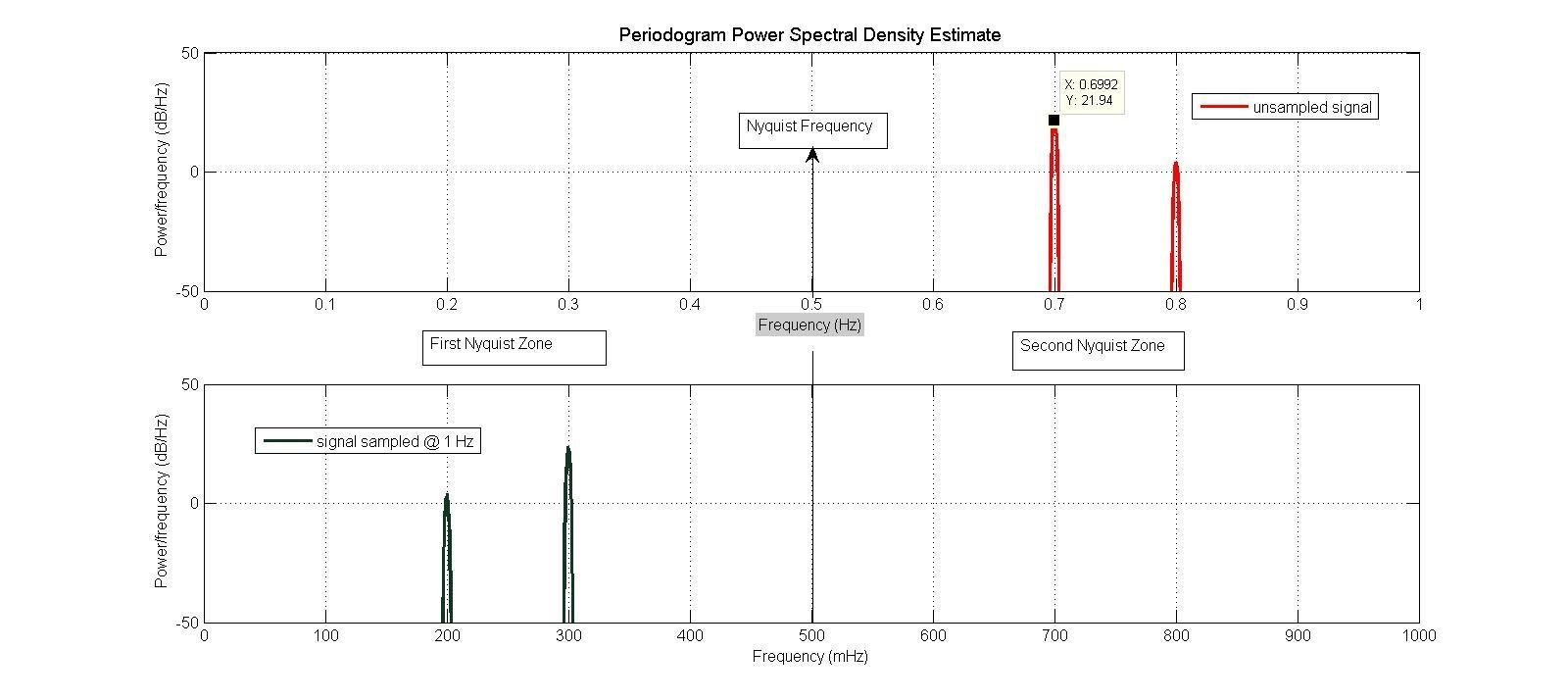
Figure 2(b). The spectra of the unsampled and sampled signal
For DACs, the output can be shaped in time to improve the performance at higher frequencies.
Figure 3(a) shows a “Normal” or “Non-Return to Zero” (NRZ) DAC output. After each sample, the output remains constant until the next sample. The analog spectrum is shown in Figure 3(b).
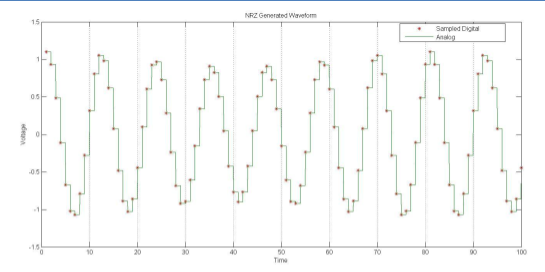
Figure 3(a). Sampling in Time Domain
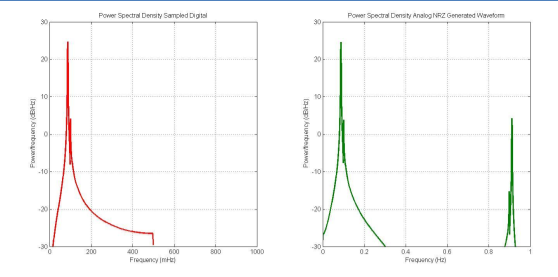
Figure 3(b).
Figure 4(a) shows a “Return to Zero” (RZ) DAC output. After each sample, the output remains constant for half a sample period, and then goes to zero. This has the effect of increasing the amplitude in the second Nyquist zone, as shown in Figure 4(b).
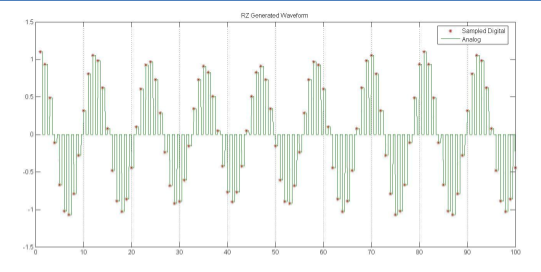
Figure 4(a). Sampling in Time Domain
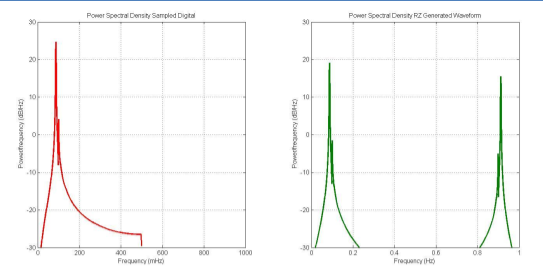
Figure 4(b).
Figure 5(a) shows a “Mix” or “RF” DAC output. After each sample, the output remains constant for half a sample period, and then goes to negative that value. This is same operation as a mixer which uses both polarities of the Local Oscillator waveform. The analog spectrum, shown in Figure 5(b), has an even larger amplitude in the second Nyquist zone. After a waveform is created via any of the above methods, the desired frequencies must be filtered out with a Low-Pass or Band-Pass filter, to remove whatever undesired alias and spurious responses there might be.
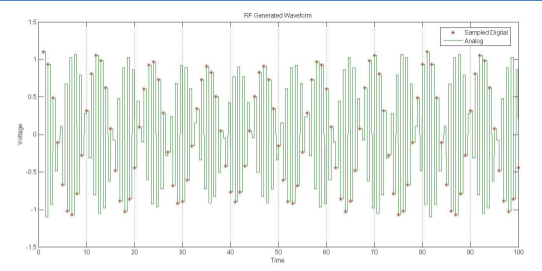
Figure 5(a). Sampling in Time Domain
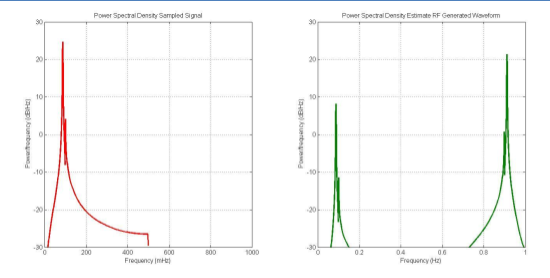
Figure 5(b).
The digital approach avoids any problems with quadrature imbalance. However, all data converters have their own undesired impartments, due to quantization and sampling effects. Some of these effects will be shown in the next article. The cost and power requirements of these high-speed data converters are also often high, compared to analog IQ networks.
Acknowledgments
When the questions addressed in this report first appeared in the author’s mind, he solicited comments through some LinkedIn groups. Several useful responses were received. Those who gave permission for their personal information to be used are; Gary Kaatz, Khaled Sayed (Consultix-Egypt), Dieter Joos (ON Semiconductor), and Jaideep Bose (Asmaitha Wireless Technologies). The author also thanks his wife, Elizabeth, who probably wondered what her husband was up to; secluded in his home office, doing work he was apparently not being paid to do.
References
The following references will be used for each of the articles in this series.
Analog IQ Modulators and Demodulators: General Descriptions
[1] Shou-Hsien Weng; Che-Hao Shen; Hong-Yeh Chang, “A wide modulation bandwidth bidirectional CMOS IQ modulator/demodulator for microwave and millimeter-wave gigabit applications,” Microwave Integrated Circuits Conference (EuMIC), 2012 7th European , vol., no., pp.8,11, 29-30 Oct. 2012 [2] Eamon Nash; “Correcting Imperfections in IQ Modulators to Improve RF Signal Fidelity “; Analog Devices Application Note AN-1039; 2009 [3] Anon; “An IQ Demodulator-Based IF-to-Baseband Receiver with IF and Baseband Variable Gain and Programmable Baseband Filtering “; Analog Devices Circuit Note CN-0320; 2013
High Speed Data Converters (DACs and ADCs); General Information
[4] Justin Munson; “Understanding High Speed DAC Testing and Evaluation”; Analog Devices Application Note AN-928; 2013 [5] Engel, G.; Fague, D.E.; Toledano, A, “RF digital-to-analog converters enable direct synthesis of communications signals,” Communications Magazine, IEEE, vol.50, no.10, pp.108, 116, October 2012 [6] Chris Pearson; “High Speed, Digital to Analog Converters Basics”; Texas Instruments Application Report SLAA523A; 2012 [7] Alex Arrants, Brad Brannon and Rob Reeder; “Understanding High Speed ADC Testing and Evaluation”; Analog Devices Application Note AN-835, 2010.
Digital IQ Modulators and Demodulators
[8] Samueli, H.; Wong, B.C., “A VLSI architecture for a high-speed all-digital quadrature modulator and demodulator for digital radio applications,” Selected Areas in Communications, IEEE Journal on, vol.8, no.8, pp.1512,1519, Oct 1990 [9] Wong, B.C.; Samueli, H., “A 200-MHz all-digital QAM modulator and demodulator in 1.2-nm CMOS for digital radio applications,” Solid-State Circuits, IEEE Journal of, vol.26, no.12, pp.1970, 1980, Dec 1991 [10] Ken Gentile; “Digital Quadrature Modulator Gain “; Analog Devices Application Note AN-924; 2009 [11] Lou, J. H.; Kuo, J.B., “A 1.5-V CMOS all-N-logic true-single-phase bootstrapped dynamic-logic circuit suitable for low supply voltage and high-speed pipelined system operation,” Circuits and Systems II: Analog and Digital Signal Processing, IEEE Transactions on, vol.46, no.5, pp.628,631, May 1999 [12] Vankka, J.; Sommarek, J.; Ketola, J.; Teikari, I; Halonen, K. A I, “A digital quadrature modulator with on-chip D/A converter,” Solid-State Circuits, IEEE Journal of, vol.38, no.10, pp.1635, 1642, Oct. 2003 [13] Yanlin Wu; Dengwei Fu; Willson, A, “A 415 MHz direct digital quadrature modulator in 0.25-nm CMOS”, Custom Integrated Circuits Conference, Proceedings of the IEEE 2003, vol., no., pp.287,290, 21-24 Sept. 2003 [14] Sommarek, J.; Vankka, J.; Ketola, J.; Lindeberg, J.; Halonen, K., “A digital modulator with bandpass delta-sigma modulator,” Solid-State Circuits Conference, 2004. ESSCIRC 2004. Proceeding of the 30th European, pp.159, 162, 21-23 Sept. 2004 [15] Lin, P.F.; Lou, J. H.; Kuo, J.B., “A CMOS quadrature modulator for wireless communication IC,” Circuits and Systems I: Fundamental Theory and Applications, IEEE Transactions on, vol.44, no.6, pp.559, 561, Jun 1997 [16] Parikh, V.K.; Balsara, P.T.; Eliezer, O.E., “All Digital-Quadrature-Modulator Based Wideband Wireless Transmitters,” Circuits and Systems I: Regular Papers, IEEE Transactions on, vol.56, no.11, pp.2487, 2497, Nov. 2009 [17] Alavi, M.S.; Staszewski, R.B.; de Vreede, L.C.N.; Long, J.R., “A Wideband13-bit All-Digital I/Q RF-DAC,” Microwave Theory and Techniques, IEEE Transactions on, vol.62, no.4, pp.732, 752, April 2014 [18] Inkol, Robert and Saper, Ron; “Digital Quadrature Modulator for Radar ESM Applications” Canadian DEFENCE RESEARCH ESTABLISHMENT OTTAWA TECHNICAL NOTE 92-10; 1992 [19] Ziomek, C.; Corredoura, P., “Digital I/Q demodulator,” Particle Accelerator Conference, 1995., Proceedings of the 1995 , vol.4, no., pp.2663,2665 vol.4,1-5 May 1995 [20] Ho, K.C.; Chan, Y.T.; Inkol, R., “A digital quadrature demodulation system,” Aerospace and Electronic Systems, IEEE Transactions on , vol.32, no.4,pp.1218,1227, Oct 1996 [21] Bravo, A; Cruz-Roldan, F., “Digital quadrature demodulator with four phases mixing for digital radio receivers,” Circuits and Systems II: Analog and Digital Signal Processing, IEEE Transactions on, vol.50, no.12, pp.1011,1015, Dec. 2003
Bandpass sampling (Rev .04 changed “subharmonic sampling” to “bandpass sampling)
[22] Parssinen, A; Magoon, R.; Long, S.I; Porra, Veikko, “A 2-GHz subharmonic sampler for signal downconversion,” Microwave Theory and Techniques, IEEE Transactions on, vol.45, no.12, pp.2344, 2351, Dec 1997 [23] Jensen, B.S.; Schmidl Sobjaerg, S.; Skou, N.; Krozer, V., “Compact front-end prototype for next generation RFI-rejecting polarimetric L-band radiometer,” Microwave Conference, 2009. EuMC 2009. European, vol., no., pp.1626, 1629, Sept. 29 2009-Oct. 1 2009 [24] Ahmed, S.; Saad El Dine, M.; Reveyrand, T.; Neveux, G.; Barataud, D.; Nebus, J. M., “Time-domain measurement system using Track & Hold Amplifier applied to pulsed RF characterization of high power GaN devices,” Microwave Symposium Digest (MTT), 2011 IEEE MTT-S International , vol., no., pp.1,4, 5-10 June 2011 [24A] Akos, D.M.; Stockmaster, M.; Tsui, J. B Y; Caschera, J., “Direct bandpass sampling of multiple distinct RF signals,” Communications, IEEE Transactions on , vol.47, no.7, pp.983,988, Jul 1999 [24B] Ching-Hsiang Tseng; Sun-Chung Chou, “Direct downconversion of multiple RF signals using bandpass sampling,” Communications, 2003. ICC ’03. IEEE International Conference on , vol.3, no., pp.2003,2007 vol.3, 11-15 May 2003
Effects of IQ Imbalance, no compensation or exploitation proposed
[25] Lopez-Martinez, F.J.; Martos-Naya, E.; Paris, J.F.; Entrambasaguas, J.T., “Exact Closed-Form BER Analysis of OFDM Systems in the Presence of IQ Imbalances and ICSI,” Wireless Communications, IEEE Transactions on, vol.10, no.6, pp.1914, 1922, June 2011 [26] Yaning Zou; Valkama, M.; Renfors, M., “Performance Analysis of Space-Time Coded MIMO-OFDM Systems Under I/Q Imbalance,” Acoustics, Speech and Signal Processing, 2007. ICASSP 2007. IEEE International Conference on, vol.3, no., pp.III-341, III-344, 15-20 April 2007 [27] Chia-Liang Liu, “Impacts of I/Q imbalance on QPSK-OFDM-QAM detection,” Consumer Electronics, IEEE Transactions on, vol.44, no.3, pp.984, 989, Aug 1998 [28] Heung-Gyoon Ryu, “Diversity Effect of OFDM Communication with IQ Imbalance in the Rayleigh Fading Channel,” Communication Software and Networks, 2010.ICCSN ’10. Second International Conference on, vol., no., pp.489, 493, 26-28 Feb. 2010 [29] Stroet, P.; “Measuring Phase and Delay Errors Accurately in I/Q Modulators”; Linear Technology Application Note 102; AN102-1; October 20057.6 Effects of IQ Imbalance, compensation or exploitation proposed
[30] Tarighat, A; Sayed, AH, “Joint compensation of transmitter and receiver Impairments in OFDM systems,” Wireless Communications, IEEE Transactions on, vol.6, no.1, pp.240, 247, Jan. 2007 [31] Marey, Mohamed; Steendam, Heidi, “Novel Data Detection and Channel Estimation Algorithms for BICM-OFDMA Uplink Asynchronous Systems in the Presence of IQ Imbalance,” Wireless Communications, IEEE Transactions on , vol.13, no.5, pp.2706,2716, May 2014 [32] Narasimhan, B.; Narayanan, S.; Minn, H.; Al-Dhahir, N., “Reduced-complexity baseband compensation of joint Tx/Rx I/Q imbalance in mobile MIMO-OFDM,” Wireless Communications, IEEE Transactions on , vol.9, no.5, pp.1720,1728, May 2010 [33] Ozdemir, O.; Hamila, R.; Al-Dhahir, N., “I/Q Imbalance in Multiple Beamforming {OFDM} Transceivers: SINR Analysis and Digital Baseband Compensation,” Communications, IEEE Transactions on, vol.61, no.5, pp.1914, 1925, May 2013 [34] Inamori, M.; Bostamam, AM.; Sanada, Y.; Minami, H., “IQ imbalance compensation scheme in the presence of frequency offset and dynamic DC offset for a direct conversion receiver,” Wireless Communications, IEEE Transactions on , vol.8, no.5, pp.2214,2220, May 2009 [35] Tarighat, A; Sayed, AH., “MIMO OFDM Receivers for Systems With IQ Imbalances,” Signal Processing, IEEE Transactions on , vol.53, no.9, pp.35833596, Sept. 2005 [36] Hai Lin; Yamashita, K., “Subcarrier allocation based compensation for carrier frequency offset and I/Q imbalances in OFDM systems,” Wireless Communications, IEEE Transactions on, vol.8, no.1, pp.18,23, Jan. 20097.7 Requirements for BaseBand DACs and ADCs
[37] Suno-Won Chung; Seung-Yoon Lee; Kyu-Ho Park, “An energy-efficient OFDM ultra-wideband digital radio architecture,” Signal Processing Systems, 2004. SIPS 2004. IEEE Workshop on, vol., no., pp.211, 216, 13-15 Oct. 2004
Requirements for RF DACS and ADCs; and for RF Non-linearities
[38] de Mateo Garcia, J.C.; Armada, AG., “Effects of bandpass sigma-delta modulation on OFDM signals,” Consumer Electronics, IEEE Transactions on , vol.45, no.2, pp.318,326, May 1999 [39] Maurer, L.; Schelmbauer, W.; Pretl, H.; Springer, A; Adler, B.; Boos, Z.; Weigel, R., “Influence of receiver front end nonlinearities on W-CDMA signals,” Microwave Conference, 2000 Asia-Pacific, vol., no., pp.249, 252, 2000 [40] Kitaek Bae; Changyong Shin; Powers, E.J., “Performance Analysis of OFDM Systems with Selected Mapping in the Presence of Nonlinearity,” Wireless Communications, IEEE Transactions on , vol.12, no.5, pp.2314,2322, May 2013 [41] Mahim Ranjan; Larson, L.E., “Distortion Analysis of Ultra-Wideband OFDM Receiver Front-Ends,” Microwave Theory and Techniques, IEEE Transactions on, vol.54, no.12, pp.4422, 4431, Dec. 2006
7.9 Carrier aggregation for LTE-advanced; Wideband spectral requirements.
[42] Pedersen, K.I; Frederiksen, F.; Rosa, C.; Nguyen, H.; Garcia, L.G.U.; Yuanye Wang, “Carrier aggregation for LTE-advanced: functionality and performance aspects,” Communications Magazine, IEEE , vol.49, no.6, pp.89,95, June 2011